|
Magnetic Fields Optional: Quantum Physics Hot Objects and Bohr's Model Bohr's Model -------------------------- our Galactic Center of Atoms and Nuclei |
One example may clarify how the "new" and "old" mechanics differ, namely the way George Gamow in 1928 explained alpha-radioactivity. As described in section #S-7 of "Stargazers" and in more detail in section #S-8 there, the atomic nucleus experiences opposing forces: the strong nuclear force holding its particles together must overcome the electric repulsion between positive protons sharing the nucleus, which tries to break it up. The nuclear force wins out at short distances, which is why nuclei exist at all, but since it falls off rapidly with distance, far away the electric repulsion dominates.
Consider a proton inside the nucleus. If something moves it a short distance away, the nuclear force pulls it right back, but if it somehow got far enough, the electric repulsion would push it away, never to return. An example is nuclear fission, possible in heavy nuclei of plutonium or uranium-235. Their nucleus contains so many protons trying to push it apart (with their electric repulsion), that adding just a modest amount energy--released when an extra neutron is allowed to be pulled into the nucleus--makes the entire nucleus break up into two positively charged chunks. These get separated far enough that they never come back again--instead, electric repulsion pushes them apart even more and releases a great amount of energy.
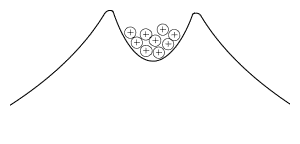
Such nuclei, and heavy nuclei close to them in mass, are all on the brink of instability, and even without externally added energy, they find a way to get rid of some of their disruptive positive charge The forces on protons inside these nuclei resemble those on a bunch of marbles inside the "crater" of a volcano-shaped surface--smooth sloping sides outside, but a moderately deep crater on top (drawing). The outline of the "mountain" can be viewed as representing the total force on protons in a nucleus. Inside the crater the attraction predominates, holding the protons together, while outside it the repulsion predominates, pushing them away. In the analogy of marbles inside a crater, if a marble could somehow get to the outside--say by carving a tunnel through the wall of the crater--this repulsion would make it roll away and it would release energy. Newtonian mechanics provides no such tunnels: the proton is imprisoned inside the crater for all eternity. According to quantum mechanics, however, the proton's location is determined by a spread-out wave function. That wave is highest inside the "crater" of the nucleus, and if the proton materializes there, it stays trapped ("if" here just helps one imagine the process; in quantum physics, if a process--like this materialization--is unobservable, it is the same as saying it does not exist). The fringes of the wave, however, extend further out, and it always has a finite (though very small) strength beyond the crater, giving a finite chance for the proton to materialize on the outside and escape. It is as if quantum laws gave it a tiny chance to "tunnel" through the barrier to the slope outside. |