|
By the last equation, as the object loses elevation--assuming nothing interferes with its motion--v2 grows, and as noted, this growth does not depend on the path taken.
This exchange between h and v2 also works in the opposite direction: an object rolling up an incline loses v2 in direct proportion to the elevation h it gains. A marble rolling down the inside of a smooth bowl gathers speed as it approaches the bottom, then as it shoots up the other side it loses all of it again. If no friction existed, it would rise again to the same height as the one from which it had started.
A simple pendulum, or a child on a swing, also trades height for v2 and back again, in the same manner. And bicycle riders are well aware that the speed gained rolling down a hillside can be traded for height when climbing the next slope. It is as if height gave us something with which we could purchase speed, and which later, if the occasion demanded, could be converted back to height.
That "something" is called energy. It was already briefly discussed in an earlier section.
This back and forth trading suggests that perhaps the sum
gh + v2/2
has a constant value: if one part decreases, the other part must get bigger. Is that sum the energy? Not quite. The effort of getting heavy load up a height h is greater than that of lifting a light one. Let us now call the amount of matter in an object its "mass. " It is obviously proportional to the object's weight, but as will later be seen, the concept of mass is more complicated than that.
If energy is to measure the effort in lifting a load, it should also be proportional to its mass m. We thus multiply everything by m and write
Energy = E = mgh + mv2/2
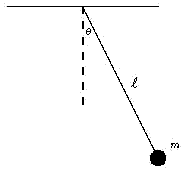
A well-known fact--already hinted at--is that in a system which does not interact with its surroundings, the total energy (denoted here by the letter E) stays the same ("is conserved"). In a pendulum at the extreme point of its swing, v = 0 and therefore the second term above vanishes, while the first term is at its biggest. Then as the mass descends descends, mv2/ 2 increases and mgh drops, until at the bottom of the swing the first term is at its smallest and the second reaches maximum. On the upswing the process reverses, and the sequence is repeated for every swing.
Both terms in the equation above have names: mgh is the potential energy, the energy of position, and mv2/2 is the kinetic energy, the energy of motion.
The exact number representing E will obviously depend on where h is measured from (the floor? sea level? the center of the Earth? ). Different choices are possible, and each leads to a different value of E: the formula is thus meaningful only if a certain reference height is chosen where h=0.
Other Kinds of Energy
Textbooks define energy as "the ability to do work" and they define work as "overcoming resistance over a distance". For instance, if m is the mass of a brick, the force on it is mg and lifting it against gravity to a height h, against the pull of gravity, requires the performance of work W, with
W = mgh
Dragging that brick a distance x along level ground against the force of friction F similarly requires the performance of work
W = Fx
The above two types of work are discussed again, in more detail, in section 18c: Work. A third type is treated in the following section #18d: Work Against an Electric Force: The Van De Graaff generator. That section also covers the generation of lightning and the clinging of projector transparencies after they emerge from a copying machine.
For the record, work is measured in joules, after James Prescott Joule (1818-89), a brewer in Manchester, England, whose experiments helped establish the fact that heat was a form of energy (see further below) and not some mysterious fluid permeating matter. Since any such work can be performed by a machine, one can also loosely define energy as anything that can cause a machine to turn.
| 
