|
En utilisant la mécanique orbitale déja vue, nous pouvons maintenant programmer (avec des approximations) une mission spatiale sur Mars. Aprés avoir construit la fusée et le vaisseau spatial, comment les orienter, et combien de temps le vol durera- il? Les orbites de la Terre et de Mars peuvent être assimilés à deux cercles dans le même plan, centrés sur le soleil. Le rayon de l'orbite de la terre, noté r1, est proche de 150.000.000 kilomètres, distance dénommée "unité astronomique" (AU). Cette unité est commode pour les mesures de distances dans le système solaire ;elle a été vue dans la section #10 sur les lois de Kepler. Ici encore, toutes les distances seront mesurées en AU et toutes les durées de temps en années. Dans ces unités, pour la terre r1 = 1 AU et T1, période orbitale, = 1 an. Pour Mars (indice inférieur 2), r2 = 1.523691, T2 = 1.8822.
Comment ne pas y aller
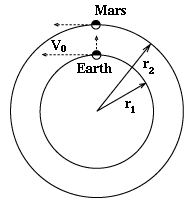
D'abord , parce que la pesanteur de la terre déforme la trajectoire pour tout vaisseau spatial lancé "en direct". Pour atténuer ce facteur , il faut d'abord placer la fusée sur une orbite autour de la terre, où la pesanteur est plus faible et la vitesse orbitale plus lente, ce qui permet de négliger ces deux facteurs. Dans la planification de l'orbite réelle, ce facteur correctif doit toujours être pris en considération. Mais même dans ce cas, la fusée reste toujours satellisée autour du soleil ,comme la terre elle même, puisqu'elle lui est directement liée, avec une vitesse d'environ 30 km/sec. Cete vitesse ,que nous écrirons V0. est beaucoup plus importante que ce qui est nécessaire pour atteindre l'orbite de Mars (et qui donc peut être plus facilement fourni par les fusées !). Si la mise à feu est effectuée lorsque Mars est au plus proche, (dessin ), V0 est perpendiculaire à la direction visée, de sorte que le vaisseau spatial se dirige dans une direction tout à fait différente de celle de Mars -- et il est certain que celui ci s'éloignera longtemps avant que ne soit couverte la distance nécessaire. C'est une deuxième raison. La troisième raison est que l'ensemble du système est dominé par l' attraction du soleil. Selon les lois de Kepler tous les objets se déplacent dans des orbites dont la trajectoire est une section conique, dont l'ellipse. En général, celles-ci sont courbes.
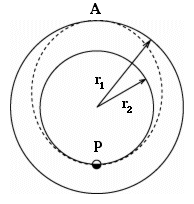
En outre, il faut coordonner vitesse et direction du vaisseau spatial à son arrivée avec celle de Mars. Ceci mène à l'ellipse de transfert de Hohmann (ou orbite), imaginée en premier lieu, en 1925, par l'ingénieur allemand Wolfgang Hohmann. C'est une ellipse dont le périhelie P (point le plus proche du soleil) est sur l'orbite de la terre et l'aphélie A (point le plus éloigné du soleil) sur celle de Mars (dessin). Une semblable ellipse de transfert, comprise entre une orbite terrestre basse (disons, r = 1.1 = 1.1 rayon terrestre) et une orbite synchrone à 6.6 RE (voir la section 21a) est fréquemment employée pour placer des satellites de communication sur leur orbites finale. Nous lançons depuis P en donnant à la fusée une vitesse supérieure à V0, ce qui la place dans une ellipse plus grande. Au moment du lancement, Mars doit être dans une position telle par rapport à la terre que le vaisseau spatial atteindra A. Pour déterminer cette position il faut connaître la durée du vol P - A, ce qui se calcule
, en utilisant la 3ème loi de Kepler, comme ci-dessous :
avec T, période orbitale et a demi grand axe, moitié de la longueur de l'ellipse orbitale (a=r dans les orbites circulaires). ). Cette constante est identique pour tous les objets satellisant le soleil, y compris naturellement la terre. Sa valeur exacte dépend des unités dans lesquelles T et a sont mesurés, et devient très simple si T est exprimé en années et a en AU (comme ici). Dans ces unités, les valeurs pour la terre dans l'équation de la troisième loi sont:
Donc
En conséquence, dans ces unités, la constante est également égale à 1. Cette valeur peut être employée avec n'importe quelle planète. En multipliant les deux côtés de l'équation par a3 (deuxième loi de l'algèbre) on obtient :
Ceci pour n'importe quelle orbite autour du soleil, y compris celui d'un vaisseau spatial dans une ellipse de transfert. La dimension PA de cette ellipse est, en AU :
C'est "l'axe principal" de l'ellipse orbitale, et la moitié de sa longueur égale le demi -grand axe a. Par conséquent :
Extraction de la racine carrée :
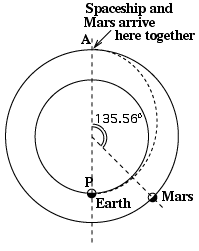
T est donc le temps aller et retour de P à A . Où doit être Mars à l'heure du lancement ? D'après les résultats cités plus haut, Mars accomplit une orbite complète, de 3600 en 1.8822 an Par conséquent, avec l' hypothèse d'une orbite circulaire et uniforme (approximation moins précise pour Mars que pour la terre), il parcourt en 0.70873 an :
Nous lançons donc quand Mars est sur son orbite à 135.5550 du point A (dessin) La prochaine section calcule la vitesse à donner à une fusée au point P afin de produire l'orbite de transfert, et les changements de vitesse exigés au point A pour synchroniser les vitesses avec Mars. Le calcul est assez long et exige de l'algèbre. |