(12a) Ancora sulla seconda legge di Keplero

Il rapporto delle velocità al perigeo e all'apogeo

    La seconda legge di Keplero descrive in che modo la velocità V di un oggetto, orbitante attorno a un singolo corpo centrale, varia lungo la sua orbita:

Come già notato nella sezione (12), ciò significa che la velocità V dell'oggetto cresce quando la sua distanza r diminuisce e viceversa.

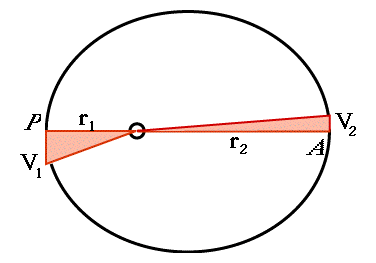
    Vi sono due punti dell'orbita in cui le direzioni di r e V sono perpendicolari tra loro: si tratta del punto P di massimo avvicinamento al corpo centrale ("perielio" per un pianeta, "perigeo" per un satellite della Terra), e del punto A di massimo allontanamento ("afelio" o "apogeo"). Siano i loro valori r₁ e V₁ in P, e r₂ e V₂ in A.

    Immaginiamo un satellite terrestre, situato al perigeo P (ved. disegno). In un secondo esso sarà avanzato di una distanza di V₁ metri (o qualunque altra unità di misura si voglia usare). Poiché si tratta di una frazione molto piccola di orbita, non si commette un grande errore se, nel calcolare l'area della superficie spazzata dal raggio vettore r₁, la sostituiamo con un segmento rettilineo. La superficie spazzata è quindi un lungo e sottile triangolo rettangolo con altezza r₁ e base V₁ (molto più sottile di quanto sia disegnato qui, per cui il disegno è solo indicativo).

    L'area A₁ di un tale triangolo, dalla formula per le aree dei triangoli rettangoli, è data dalla metà della base per l'altezza, cioè

    Similmente, l'area A₂ coperta in un secondo dopo il passaggio all'apogeo A è uguale a

Tuttavia, per la seconda legge di Keplero A₁ = A₂ per cui

e moltiplicando entrambi i membri per 2

Una forma più pratica di questa relazione si ottiene se dividiamo ambo i membri per V₂r₁ :

    Il rapporto delle velocità è uguale all'inverso del rapporto delle distanze. Cioè, più è piccola la distanza, più è veloce il moto. Se la distanza al perigeo è la metà della distanza all'apogeo, la velocità al perigeo sarà il doppio di quella all'apogeo. (Ma, attenzione, questa proporzionalità vale solo per i punti P e A, non per gli altri punti dell'orbita).

Perché le stagioni hanno durate diverse?

    Ma è veramente così?

    L'equinozio di primavera del 2003 è stato il 21 marzo, mentre l'equinozio autunnale è stato il 22 settembre, 184 giorni dopo. Nel 2004, un anno bisestile, l'equinozio di primavera è stato il 20 marzo, e, se si contano i giorni, si vede che sono passati soltanto altri 181 giorni. I due intervalli non sono quindi uguali.

    Come può essere? Le posizioni degli equinozi si trovano nei punti opposti dell'orbita terrestre, a 180° di distanza, eppure l'inverno (nell'emisfero boreale) è durato tre giorni di meno dell'estate.

    A causa della seconda legge di Keplero, la Terra si muove un po' più rapidamente durante l'inverno. Come è stato fatto notare alla fine della sezione "Le stagioni dell'anno", e anche in connessione con la teoria di Milankovich a proposito delle ere glaciali, la Terra si trova nel punto di massima vicinanza al Sole (al "perielio") attorno al 4 gennaio. Dalle equazioni discusse sopra, risulta che è quello è il periodo dell'anno in cui la Terra si muove più velocemente. Inoltre (ved. disegno), la metà dell'ellisse più vicina al Sole è anche un po' più corta. Per la Terra la differenza è piccola, poiché la sua orbita è quasi circolare, ma tuttavia esiste ed è questo il motivo dei 3 giorni di differenza.