(12b) Come si calcola un moto orbitale

    Come si è visto precedentemente, il moto di un satellite (o di un pianeta) lungo la sua orbita ellittica è specificato da 3 "elementi orbitali":

(1) Il semiasse maggiore a, la metà della dimensione più lunga dell'ellisse orbitale, che specifica la grandezza dell'orbita.

(2) L'eccentricità e, un numero compreso tra 0 e 1, che specifica la forma dell'orbita. Per una circonferenza e = 0, e valori più grandi corrispondono a circonferenze sempre più schiacciate, fino ad arrivare a e = 1 per cui l'ellise si dilata all'infinito e diventa una parabola. Le orbite di tutti i maggiori pianeti sono molto prossime a circonferenze: per l'orbita della Terra, per esempio, si ha  e = 0,0167

(3) L'anomalia media M, un angolo che cresce a ritmo costante, aumentando di 360 gradi ogni orbita

M = M(0) + 360°(t/T)

dove M(0) è il valore di M al tempo t = 0 e T è il periodo orbitale. Con questi dati, si può calcolare rapidamente M per ogni istante di tempo t.

    Tuttavia, l'effettiva posizione del satellite è data dall'anomalia vera  f. In coordinate polari (r,f) che descrivono il moto del satellite nel suo piano orbitale,   f   è l'angolo polare. L'equazione dell'orbita è

r = a(1 – e²)/(1 + e cos f)

    Anche l'angolo f cresce di 360^o ogni orbita completa, ma non a velocità uniforme. Per la legge della aree di Keplero, essa cresce rapidamente vicino al perigeo (il punto più vicino alla Terra) ma lentamente vicino all'apogeo (il punto più lontano).

    Le informazioni necessarie per ricavare f ad ogni istante t sono contenute nella legge delle aree, ma il calcolo effettivo non è facile. Il procedimento richiede l'uso di un angolo ausiliario, l'anomalia eccentrica E che, come f e M aumenta di 360^o ogni orbita. Al perigeo tutte e tre le anomalie sono uguali a zero.

    Il disegno qui a destra mostra una costruzione geometrica di questi angoli (non cercate di entrare troppo nei dettagli). L'ellisse orbitale è inscritta in una circonferenza di raggio a, e, per una data posizione P del satellite, si può disegnare su tale circonferenza un corrispondente punto Q, che ha in comune lo stesso segmento perpendicolare all'asse dell'ellisse. Allora E è l'angolo tra l'asse maggiore dell'ellisse e la linea tracciata dal centro della circonferenza a Q ("eccentrica" può significare qui "dal centro").

L'equazione di Keplero

    Supponiamo ora di conoscere gli elementi a, e e M(0) al tempo t=0, e di voler trovare il valore di f in un altro istante di tempo t. Se il valore di f è noto, l'equazione precedente fornisce r, e la coppia di valori (r, f) specifica la posizione del satellite nel suo piano orbitale. Il primo passo è quello di ricavare

M = M(0) + 360°(t/T)

    Assumiamo che il periodo T sia noto (questo argomento richiede la terza legge di Keplero ed è discusso, per le orbite circolari, nelle sezioni 20 e 20a). Si può dimostrare che l'angolo E soddisfa "l'equazione di Keplero"

M = E – (180°/p)e sinE

dove p = 3,14159256... è il rapporto tra la circonferenza e il suo diametro. Come mai adesso esce fuori questo numero, potreste chiedere? Il fatto è che la divisione di una circonferenza in 360 gradi può essere conveniente per certi usi (l'abbiamo ereditata dagli antichi babilonesi) ma il numero 360 non ha una particolare collocazione in matematica. Probabilmente è collegato al numero di giorni in un anno. La divisione "naturale" degli angoli, che si usa nei calcoli e in altri rami della matematica, è quella in radianti, con 360 gradi uguali a 2p = 6,2831... radianti (per cui un radiante è circa uguale a 57,3 gradi). Con gli angoli espressi in radianti, l'equazione di Keplero si semplifica in

M = E – e sinE

    Qualunque sia la forma usata, la matematica non conosce nessun modo per esprimere direttamente E in funzione di M. Tuttavia si può approssimare la soluzione con l'accuratezza desiderata mediante l'iterazione, cioè iniziando con una soluzione approssimata, e poi migliorandola sempre di più con un opportuno procedimento ("algoritmo" -- per saperne di più circa l'origine di questa parola ved. qui). Se l'eccentricità e non è troppo grande, cioè se l'ellisse non è molto diversa da una circonferenza, allora M e E non sono molto diverse tra loro. Pertanto una congettura iniziale

E' = M

può non essere molto lontana dal vero. Inserendo questo valore "di congettura" nel termine sinE si ottiene un valore un po' migliore E"

E" = M + (180°/p)e sinE'

    Ora si può inserire E" nel termine sinE e ottenere un'approssimazione ancora più vicina, e così via... fino a che le prime (diciamo) dieci cifre decimali del valore di E non cambiano più. A quel punto possiamo decidere di avere trovato E con un'accuratezza sufficiente da poter interrompere il procedimento. Con i calcolatori un tale procedimento di miglioramenti successivi ("iterazione di una soluzione", che è un tipo di algoritmo) converge molto rapidamente. Esistono anche altri metodi sufficientemente veloci anche in casi in cui e non sia molto piccola.

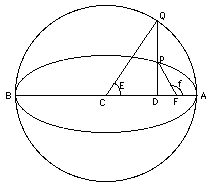
Una volta trovato il valore di E, esistono varie formule per ottenere l'anomalia vera f. Per esempio, si può prima ricavare

r = a(1 – e cos E)

e quindi cos f può essere ottenuto da

r = a(1 – e²)/(1 + e cos f)

e sin f si ricava poi da cos f. Tutto questo viene oggi calcolato automaticamente, ma deve essere stata una bella fatica prima dell'avvento dei calcolatori.

L'orbita nello spazio

1. L'inclinazione i.
2. L'argomento del perigeo ω (la lettera greca omega minuscola).
3. La longitudine del nodo ascendente Ω (omega maiuscola).

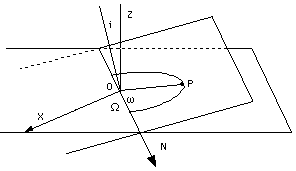
    Per orientare l'orbita nello spazio tridimensionale, occorre un piano e una direzione di riferimento. Per le orbite dei satelliti, il piano di riferimento -- il piano orizzontale, nel disegno -- è in genere il piano equatoriale terrestre (qualche volta è il piano dell'eclittica). La direzione di riferimento in entrambi i casi è la direzione dal centro della Terra all'equinozio di primavera (che si trova su entrambi quei piani). Chiameremo questa direzione la direzione x, poiché è questo il suo ruolo nel sistema di coordinate (x,y,z) usato nei calcoli orbitali.

    Due piani non paralleli si intersecano sempre lungo una retta, nel modo in cui il piano di una porta interseca il piano della parete lungo i cardini della porta. Anche il piano orbitale e il piano equatoriale (usato come riferimento) si intersecano in tal modo, e la loro intersezione è chiamata la linea dei nodi N. Facciamo coincidere l'origine O del nostro sistema di coordinate con il centro della Terra, che è anche il fuoco dell'ellisse. Questo punto appartiene sia al piano equatoriale che al piano orbitale, e quindi si trova anche sulla linea N in cui i due piani si intersecano (ved. disegno). E perciò...

1. L'inclinazione i è l'angolo di apertura della "cerniera" lungo la linea N. Si definisce meglio tracciando da O due linee perpendicolari ai rispettivi piani (equatoriale e orbitale) e misurando l'angolo tra di esse (ved. disegno).

2. L'angolo Ω è misurato nel piano equatoriale tra N e la direzione di riferimento x. Si può immaginare di ruotare la "cerniera" N attorno al punto O, senza cambiare l'inclinazione: il piano orbitale allora ricopre tutti i possibili valori di Ω.
   Ma perché si chiama "nodo ascendente"? La definizione data sopra è in realtà un po' ambigua: N definisce due linee che partono da O, in direzioni opposte. Da quale delle due va misurato Ω? Per risolvere questo dilemma, notiamo che il piano equatoriale divide lo spazio in due parti, una a nord e una a sud di tale piano. Specificando "nodo ascendente", si sceglie il ramo in cui il satellite, attraversandolo, entra nel semispazio settentrionale, anziché il ramo in cui lo abbandona.

3. Infine, ω è l'angolo misurato nel piano orbitale tra N e la direzione che va da O al perigeo (punto P). Se il perigeo si trova sulla "cerniera", dalla parte delle x positive, allora ω = 0. Ruotando l'orbita di 90^o fino a che la linea OP sia perpendicolare a N, si ottiene ω = 90^o; ruotandola ulteriormente fino a che raggiunga la parte negativa delle x, si ottiene ω = 180^o.

    Supponiamo di conoscere gli elementi orbitali di un certo satellite, per esempio, la navetta spaziale (questi dati si trovano spesso su Internet). I primi tre (a, e, M), con M riferita a un particolare istante di tempo, consentono di calcolare dove si trova il satellite a un certo istante lungo la sua orbita. Con (i, ω, Ω) si può poi trovare dove l'oggetto si trova nel cielo.

    [Chi desiderasse saperne di più sul modo in cui si calcolano tali rotazioni nello spazio tridimensionale può consultare il problema n.8 degli "esercizi di trigonometria". Questo problema considera soltanto le rotazioni in due dimensioni (per esempio, su un foglio di carta), ma vi è un collegamento a una breve sezione aggiuntiva, in cui viene spiegato come estendere il procedimento al caso tridimensionale.]