|
to Galileo Kepler's Laws (For teachers) and First Law Newtonian Mechanics |
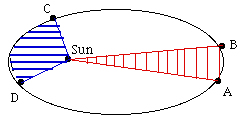
The LawThe ellipse traced by a planet around the Sun has a symmetric shape, but the motion is not symmetric. Think of a stone thrown upwards. As it rises it loses speed... then for an instant, at the top of the trajectory, it moves very slowly... and finally it comes down, gathering speed again. In many ways, a planet around the Sun, or of a scientific satellite around Earth, moves like that, too, although the equations are different. That is most evident if the orbit is elongated, that is, its eccentricity is large. As the planet or satellite rises in its orbit, it slows down, then as it returns, it speeds up again. It moves fastest during its closest approach, at a point of the orbit called perihelion for a planet ("helios" is the Sun) and perigee for an Earth satellite ("gee" from "geo", denoting Earth-related). After studying actual observations, mainly of Mars, Kepler proposed the following prescription for predicting the speeding-up and the slowing-down. Let a line ("radius vector") be drawn from the center of the Sun to the planet (or from the center of Earth to the satellite). Kepler's law states: "The radius vector sweeps equal areas in equal times"
As an example, let the drawing on the right represent the orbit of an Earth satellite, and let AB and CD be the portions of the orbit covered in 3 hours near apogee and near perigee, respectively. If then O is the Earth's center, the shaded areas OAB and OCD are equal. What it means, obviously, is that CD is much longer than AB, because near perigee the satellite moves much faster and it covers a much greater distance in 3 hours. |