Un altro metodo di calcolo -- più breve, più elegante e più generale, ma che usa i vettori e la rotazione dei sistemi di riferimento -- viene presentato nella sezione (34c). Gli altri due punti lagrangiani, L4 e L5, giacciono sull'orbita della Terra, e le linee che li congiungono al Sole formano angoli di 60° con la linea Terra-Sole. In questi punti, un calcolo basato sui due corpi Terra e Sole predice ancora uno stato stazionario (cioè di equilibrio in un sistema di riferimento che ruoti insieme alla Terra). Anche qui, tuttavia, L4 e L5 sono così lontani che, per un calcolo realistico del moto di un'astronave posizionata nelle loro vicinanze, occorre includere l'attrazione di altri pianeti. Inoltre, anche il sistema Terra-Luna ha i suoi punti L4 e L5, e tali punti sono stati presi in considerazione come possibili posizioni in cui collocare osservatori e "colonie spaziali" autosufficienti. Essi hanno una importante proprietà (che non verrà qui dimostrata): che sono stabili. Al contrario, l'equilibrio nei punti L1 e L2 è instabile, come quello di una piccola biglia posta sopra una grossa sfera. Se viene posizionata esattamente sulla sommità della sfera, la biglia resta ferma, ma il minimo urto la farà allontanare sempre di più dalla sua posizione di equilibrio, finché cadrà giù. Diversamente, l'equilibrio in L4 e in L5 corrisponde a quello di una biglia posta in fondo a una scodella sferica: se riceve una piccola spinta, rotolerà di nuovo nella sua posizione iniziale. Perciò un'astronave in L4 o in L5 non tende ad allontanarsi dalla sua posizione, mentre se si trovasse in L1 o in L2 sarebbe necessario dotarla di piccoli razzi per riportarla di tanto in tanto nella sua posizione di equilibrio. Mostreremo ora che i punti L4 e L5 del sistema Terra-Luna sono posizioni di equilibrio in un sistema di riferimento che ruota con la Luna, supponendo che l'orbita lunare sia circolare. Orbite non circolari e il problema della stabilità sono argomenti che esulano dalla presente trattazione.
Gli strumenti di calcolo
ed è facile verificare che la somma di queste due distanze è uguale a c e che il loro rapporto è m/M. Una forma alternativa di DB (che sarà utile in seguito) si ottiene dividendo numeratore e denominatore per M:
Dalla trigonometria utilizzeremo il "teorema dei seni". Supponiamo di avere un triangolo ABC di dimensioni e forma arbitrarie (ved. figura). Gli angoli nei tre vertici saranno indicati con A, B e C, mentre le lunghezze dei lati opposti a ciascuno dei vertici saranno indicate con a, b e c. Allora il teorema dei seni afferma
sinA = h/ b b sinA = h e dividendo entrambi i membri per ab si ottiene il risultato richiesto. Per dimostrare che anche l'angolo C soddisfa questa condizione, ripetiamo il calcolo conducendo il segmento perpendicolare dal vertice A o dal vertice B. Ci occorre anche l'identità trigonometrica per il seno della somma di due angoli. Se indichiamo i due angoli con le lettere greche α e β
La dimostrazione di questa identità viene data separatamente. Infine utilizzeremo le regole di scomposizione dei vettori (ved. la sezione 14). Supponiamo che una forza F agisca su un oggetto posto nel punto C, formando un angolo α con la direzione di una data linea, indicata qui con R (ved. figura). Supponiamo anche di dover scomporre F nelle due componenti parallela e perpendicolare a R. Nel triangolo CPQ, se CP rappresenta la forza F, allora CQ e QP rappresentano le sue componenti parallela e perpendicolare. Quindi, poiché
Le condizioni di equilibrio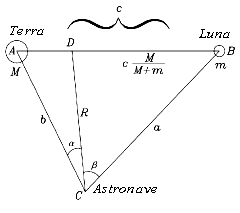
Alla figura riportata precedentemente per illustrare il centro di massa del sistema Terra-Luna, aggiungiamo ora un'astronave in un certo punto C, a una distanza b dalla Terra, a dalla Luna e R dal centro di massa D. Come nella derivazione del teorema dei seni, chiamiamo (A,B,C) gli angoli nei vertici indicati con queste lettere, e chiamiamo (a,b,c) le lunghezze dei lati opposti ai vertici (A,B,C).Indichiamo inoltre con (α,β) le due parti in cui R divide l'angolo C. Verificare tutto questo prima di andare avanti. La domanda a cui dobbiamo rispondere è: Sotto quali condizioni l'astronave nel punto C mantiene fissa la sua posizione rispetto alla Terra e la Luna? Per svolgere meglio il calcolo, è opportuno considerare un sistema di riferimento che ruoti con la Luna. In tale riferimento, se un satellite nel punto C è in equilibrio, esso manterrà sempre la stessa distanza sia dalla Terra che dalla Luna. Il centro di rotazione è il punto D (anche la Terra vi ruota intorno) e, se l'astronave in C è in equilibrio, tutti e tre i corpi avranno lo stesso periodo orbitale T. Se C è immobile nel sistema di riferimento rotante, non esisterà una forza di Coriolis (che agisce soltanto su oggetti che si muovano rispetto a un tale sistema di riferimento), ma l'astronave sarà soggetta a una forza centrifuga, come la Luna e la Terra.
Raccogliamo ora le equazioni-- quelle a cui devono obbedire le distanze e gli angoli.
(1) Notiamo dapprima che il raggio di rotazione R dell'astronave sarà Indicando la velocità di rotazione della Luna con V e quella dell'astronave con v, poiché distanza = velocità × tempo
Le due espressioni sono entrambe uguali a 2π/ T e devono quindi essere uguali tra loro, per cui (1) v/R = (V/c)(1 + m/M) Questo esprime semplicemente la ben nota osservazione che, se due oggetti ruotano solidalmente, quello più lontano dall'asse si muoverà più velocemente, e le loro velocità saranno proporzionali alle loro distanze dall'asse di rotazione.
(2) La forza centrifuga sulla Luna è
(2) GM/c = V2 (1 + m/M)
(3) Sia m' la massa dell'astronave. La forza centrifuga su di essa è
Ora, per la teoria della gravitazione di Newton
Sostituendo questi valori nell'espressione precedente e dividendo entrambi i membri per m' si ottiene la 3a equazione: (3) v2/R = (Gm/a2) cosβ + (GM/b2) cosα
(4) Infine, le componenti delle forze che attraggono l'astronave in direzione perpendicolare a R devono annullarsi. Altrimenti l'astronave sarebbe attratta da quella più grande delle due e non rimarrebbe ferma in C, e quindi non sarebbe più in equilibrio. Questo richiede che
(4) (m/a2) sinβ = (M/b2) sinα
Raccogliamo ancora una volta tutte le equazioni:
Le quantità che compaiono qui sono di 3 tipi.
Avevamo già effettuato una eliminazione precedentemente, nel caso in cui vi erano due equazioni contenenti il periodo orbitale T. Dopo aver risolto entrambe le espressioni rispetto a 2π/T, e uguagliato i secondi membri, avevamo ottenuto un'espressione che non conteneva più T (in un processo di eliminazione, "si rinuncia sempre a una delle due equazioni": si parte con due e si finisce con una sola equazione). Il procedimento è quindi il seguente. Elimineremo V tra la (1) e la (2), lasciando una equazione contenente soltanto v. Successivamente elimineremo v tra l'equazione ottenuta e la (3), arrivando così ad una equazione che non contiene più le velocità -- oltre alla (4), che neppure contiene né V né v. Dalla (1), elevando al quadrato entrambi i membri
Moltiplicando ambo i membri per c2 e dividendoli per (1 + m/M)
Ma, per la (2) Uguagliando le due espressioni: (5) v2 (c2/R2) /[1 + m/M] = GM/c e V è stata eliminata. Adesso moltiplichiamo ambo i membri per (1 + m/M), dividiamoli per c2 e moltiplichiamoli poi per R
E quindi (moltiplicando R per il fattore 1/c)
Dividendo tutto per GM si ottiene una delle equazioni desiderate, mentre l'altra è la (4): (6) (1/c2) (R/c) (1 + m/M) = (1/a2)(m/M) cosβ+ (1/b2) cos α (4) (m/a2) sinβ = (M/b2) sinα Piuttosto complicato! Tuttavia già abbiamo dato una sbirciata alla risposta e sospettiamo che le cose andranno bene se il triangolo ABC è equilatero, cioè se tutti i suoi angoli sono di 60° e tutti i suoi lati hanno la stessa lunghezza, che indicheremo con r:
In tal caso, se moltiplichiamo le equazioni precedenti per r2, tutti i fattori (1/a2), (1/b2) e (1/c2) spariranno, lasciando (7) (R/c)(1 + m/M) = (m/M)cosβ + cosα (8) m sinβ= M sinα Da cui m/M = sinα/sinβ Sostituendo questo valore nel secondo membro della (7)
Moltiplicando poi per sinβ sin β (R/c)(1 + m/M) = sinαcosβ+ cosαsinβ = sin(α + β) = sin C = sin B
L'ultima relazione deriva dal fatto che tutti e tre gli angoli (A,B,C) sono uguali. Questa d'altronde non è altro che il legge dei seni applicata al triangolo CDB e quindi è ovviamente soddisfatta. Andando a ritroso da questa relazione, possiamo ora mostrare che tutte le precedenti equazioni, dalla (1) alla (4), sono soddisfatte se il triangolo ABC è equilatero. Pertanto C è un punto di equilibrio nel sistema di riferimento rotante. Se avessimo assunto che il triangolo ABC non fosse equilatero e che le distanze (a,b,c) non fossero uguali, avremmo ottenuto una relazione diversa dalla legge dei seni, e quindi non valida. Perciò tutte le equazioni richieste per l'equilibrio nel punto C non sarebbero soddisfatte.
Come è stato già accennato, poiché L4 e L5 sono punti di equilibrio stabile, tali punti sono stati proposti come locazioni per "colonie spaziali" autosufficienti, un'idea sviluppata e sostenuta dal defunto Gerald O'Neill. Nel 1978 Bill Higgins and Barry Gehm scrissero perfino, per i potenziali abitanti di tali colonie spaziali, la "Canzone dell'L5" ("Home on Lagrange", La casa nel punto di Lagrange) sull'aria della canzone "Home on the Range" (La casa nella fattoria). Questo è l'inizio:
Home on Lagrange (La casa nel punto di Lagrange)
Dove i gravitoni si concentrano Dove il problema dei tre corpi è risolto Dove le microonde liete vi entrano Fino a tre gradi sullo zero assoluto Così freddo che nessun virus si è evoluto.
CORO:
Ulteriori approfondimenti:A proposito di colonie spaziali nei punti lagrangiani:
A proposito dei punti L4 e L5, e degli asteroidi bloccati nelle vicinanze dei punti L4 e L5 del sistema Sole-Giove: "When Trojans and Greeks Collide" (Quando i Greci e i Troiani si scontrano); di I. Vorobyov, Quantum, Settembre-Ottobre 1999, p. 16-19. Questo articolo contiene un'altra dimostrazione delle proprietà di equilibrio nei punti L4 e L5, più generale (senza limitazioni di massa) ma che fa uso di sistemi di riferimento rotanti e di vettori bidimensionali. Il calcolo è esposto nella sezione (34-c) di questo sito Web. |
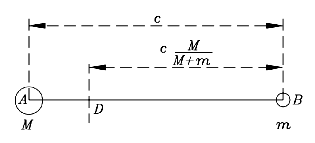Come è mostrato nella 
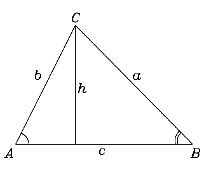Dimostriamolo per gli angoli A e B, conducendo dal vertice C il segmento perpendicolare al lato del triangolo opposto a quel vertice. Sia h la lunghezza di tale segmento. Allora