|
Usando le nozioni di meccanica orbitale sviluppate precedentemente, possiamo ora progettare (con alcune approssimazioni) una missione spaziale verso Marte. Supponendo di avere a disposizione un veicolo spaziale con motori a razzo, come lo dovremo dirigere e quanto tempo durerà il viaggio? Supponiamo, facendo qualche approssimazione, che le orbite della Terra e di Marte siano entrambe circolari e che giacciano sullo stesso piano, con il Sole nel centro. Il raggio dell'orbita terrestre, che indicheremo con r1, è pari a circa 150·000·000 chilometri, una distanza che è nota come unità astronomica (UA). È questa una conveniente unità di misura per le distanze del Sistema Solare ed è stata usata nella sezione #10 sulle leggi di Keplero. Come in quella sezione, anche qui tutte le distanze verranno misurate in UA e tutti i tempi in anni. Con tali unità di misura, per la Terra è r1 = 1 UA e il periodo orbitale è T1 = 1 anno. Per Marte (con indice 2), r2 = 1,523691, T2 = 1,8822.
Come non andare
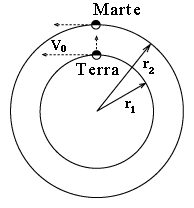
Primo, la gravità terrestre incurverebbe la traiettoria di ogni veicolo spaziale lanciato da qui. Per eliminare questo fattore, supponiamo che il razzo sia stato già immesso su un'orbita lontana attorno alla Terra, dove la gravità terrestre sia debole e il moto orbitale sia lento, così da poter trascurare entrambi questi effetti. In un reale calcolo orbitale, tali effetti devono sempre essere presi in considerazione per fare delle correzioni. Anche così, però, il razzo sarebbe ancora in orbita attorno al Sole insieme alla Terra, a cui resta comunque debolmente attaccato, muovendosi a circa 30 km/sec, una velocità che indicheremo con V0. Questo moto è molto più veloce di quanto ci occorre per raggiungere l'orbita di Marte (o che potrebbe essere ottenuto con l'aiuto di motori a razzo!). Se il razzo viene lanciato quando Marte è nel punto più vicino alla Terra (ved. disegno), V0 è in direzione trasversale rispetto alla direzione di puntamento, per cui il razzo partirà in una direzione molto diversa da quella diretta verso Marte, e inoltre Marte si sarà spostato molto prima che si sia percorsa la distanza dal pianeta. Questo è il secondo motivo.
Il terzo motivo è che l'intero sistema è dominato dalla gravità solare. Tutti gli oggetti si muovono lungo orbite (o traiettorie) che, per le leggi di Keplero, sono parti di sezioni coniche, e -- in questo caso -- ellissi. In generale, di tratta di traiettorie curve.
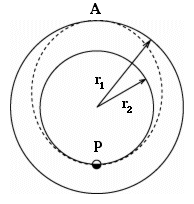
Inoltre, occorre coordinare la velocità e la direzione dell'astronave, al momento dell'arrivo, con quelle di Marte. Questo porta alla cosiddetta ellisse di trasferimento di Hohmann (o orbita di trasferimento), proposta per la prima volta nel 1925 dall'ingegnere tedesco Wolfgang Hohmann. Si tratta di un'ellisse in cui il perielio P (il punto più vicino al Sole) sta sull'orbita della Terra e l'afelio A (il punto più lontano dal Sole) sta su quella di Marte (ved. disegno). Una simile ellisse di trasferimento, tra un'orbita bassa intorno alla Terra (diciamo, r = 1,1 RT = 1,1 Raggi Terrestri) e l'orbita geostazionaria a 6,6 RT (ved. sezione 21a), viene spesso usata per immettere i satelliti per le comunicazioni nella loro orbita definitiva. Il lancio avviene dal punto P dando al razzo una ulteriore velocità oltre a quella V0, inserendolo quindi in una ellisse più grande.
Marte deve trovarsi, al momento del lancio, in una posizione, rispetto alla Terra, tale che raggiunga il punto A nello stesso momento in cui tale punto sarà raggiunto dall'astronave. Per determinare una tale posizione occorre conoscere la durata del volo da P ad A, e questa verrà ricavata adesso, usando la terza legge di Keplero.
dove T è il periodo orbitale e a il semiasse maggiore dell'orbita, pari alla metà della lunghezza dell'ellisse (a=r per orbite circolari). La costante è la stessa per tutti gli oggetti in orbita attorno al Sole, inclusa naturalmente la Terra. Il suo esatto valore dipende dalle unità di misura usate per T e a. Tale valore diventa molto semplice se T è misurato in anni e a in UA (come viene fatto qui). Inserendo nell'equazione della 3ª legge i valori relativi alla Terra si ha
Quindi, nelle nostre unità
Di conseguenza, in queste unità anche la costante è uguale a 1, e questo valore può essere usato per ogni pianeta. Moltiplicando entrambi i membri dell'equazione per a3 (seconda legge algebrica)
Anche questo vale per ogni orbita intorno al Sole, inclusa quella di un'astronave su una ellisse di trasferimento. La lunghezza PA di tale ellisse è, in UA:
Questo è "l'asse maggiore" dell'ellisse orbitale, e la metà della sua lunghezza è uguale al semiasse maggiore a. Quindi
Estraendo la radice quadrata
Questo è il tempo per andare da P ad A e di nuovo indietro fino a P. Il tempo di sola andata verso Marte è quindi la metà, cioè 0,70873 anni o circa 8,5 mesi.
Dove dovrebbe trovarsi Marte al momento del lancio? Dai numeri citati all'inizio di questa sezione, Marte impiega 1,8822 anni a compiere un'orbita intera di 360o. Pertanto, assumendo un'orbita circolare e un moto uniforme (un'approssimazione che è un po' meno accurata per Marte di quanto non lo sia per la Terra), in 0,70873 anni Marte dovrebbe percorrere
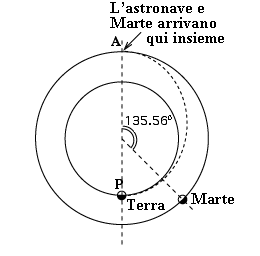
Quindi effettueremo il lancio quando Marte, nella sua orbita, è 135,555o lontano dal punto A (ved. disegno). Nella prossima sezione verrà calcolata la velocità che il razzo deve possedere nel punto P per ottenere un'orbita di trasferimento, e la variazione di velocità richiesta nel punto A per sincronizzare la sua velocità con quella di Marte. Questo calcolo è più lungo e richiede un po' di nozioni di algebra. |