Las Tres Leyes de Kepler del Movimiento Planetario

    Abajo encontrará una conferencia dada el 23 de Marzo de 2005, a maestros de ciencia del condado Anne Arundel, Maryland. Esta contiene una repaso de las leyes de Kepler con ejemplos, aplicaciones, problemas e historia relacionada al tema, un recurso de material de clase.
    Está indexada y ligada a secciones apropiadas de "De Astrónomos a Naves Espaciales". A los maestros también les fueron dados discos con el material de la red, permitiéndoles que lo puedan acceder estando desconectados del internet.

   Una guía rápida a las secciones de "Astrónomos" relacionadas con las leyes de Kepler pueden ser encontradas en la sección "Leyes de Kepler". En las líneas que siguen, esas secciones algunas veces serán referidas por sus números. También puede tener acceso a la lista completa de vínculos, ya sea desde el "Mapa del Sitio" en la parte superior de esta página o desde "De Regreso a la Lista Maestra" al final del artículo.

    El disco tiene más material del que alguna vez podrá ser cubierto en su clase. Pero ustedes son los maestros, y necesitan un conocimiento más amplio--permitiéndole escoger y seleccionar material de acuerdo a las circunstancias, y mencionar datos curiosos sin una discusión detallada, tan solo para crear interés.

    Y si usted corre con mucha suerte, encontrará en su clase un alumno o dos que en realidad desean conocer más. A aquellos los puede enviar aquí, a la red, para recibir una educación más completa.

    Permítame enfocarme en tres aspectos:
---¿Qué son? las leyes de Kepler, ¿qué significan?, y ¿porqué? son importantes.

Las leyes fueron formuladas entre 1609 y 1619, y son (como normalmente se enuncian):

1. Los planetas se mueve alrededor del Sol en elipses, estando el Sol en un foco
2. La línea que conecta a Sol con un planeta recorre áreas iguales en tiempos iguales.
3. El cuadrado del período orbital de un planeta es proporcional al cubo (tercera potencia) de la distancia media desde el Sol
       (o dicho de otra manera--desde el "semieje mayor" de la elipse, la mitad de la suma de la distancia mayor y menor desde el Sol).

La Importancia de las Leyes de Kepler

    Las leyes de Kepler describen el movimiento de los planetas alrededor del Sol.
Kepler sabía de la existencia de 6 planetas: Tierra, Venus, Mercurio, Marte, Júpiter y Saturno.

La órbita de la Tierra alrededor del Sol. Esta es una vista en perspectiva, la forma verdadera de la órbita es muy cercana a un círculo.

    Todos ellos (incluso la Luna) se mueven muy cercanamente al mismo plano (sección #2 de "Astrónomos"). El sistema solar es ¡plano como una tortilla!. La Tierra está sobre la tortilla también, de manera que vemos al sistema completo de perfil--la tortilla completa ocupa una línea (o tal vez una banda pequeña) haciendo un corte en el cielo, conocido como la eclíptica. Cada planeta, la Luna y el Sol también, se mueven a lo largo o cercano a la eclíptica. Si observa un montón de estrellas brillantes unidas en una línea alrededor del cielo--y la línea tal vez contenga también a la Luna, (cuya órbita están también cercana a esa "tortilla"), o el lugar en el horizonte por donde el Sol se acaba de ocultar--es probable que esté viendo planetas.

    Los antiguos astrónomos creían que la Tierra era el centro del Universo--las estrellas estaban sobre una esfera rotando alrededor de ella (ahora sabemos, que la Tierra es la que en realidad gira) y los planetas se movían en sus propias "esferas de cristal" en maneras graciosas. Normalmente se movían en la misma dirección, pero algunas veces su movimiento se invertía por un mes o dos, y nadie sabía por qué.

    Un clérigo Polaco llamado NicolásCopérnico observó alrededor de 1543 que dichos movimientos tenían sentido si los planetas se movían alrededor del Sol, si la Tierra era uno de ellos, y si los más distantes se movían más lentamente--de manera que algunas veces la tierra los rebasaba, y eso hacía parecerles que se retrasaban por un tiempo. Las órbitas de Venus y Mercurio estaban dentro de la de la Tierra, de manera que ellos nunca se mueven muy lejos del Sol. Razón por la cual usted ¡nunca ve a Venus a medianoche!

    Espero que usted, al describirle esas características--la "tortilla de la eclíptica, el movimiento hacia atrás ("retrógrado"), Venus siempre cerca del Sol--a sus estudiantes, ellos obtengan una apreciación de la apariencia de los planetas en el cielo, como estrellas brillantes que se mueven a lo largo del mismo camino que el Sol y la Luna. Las 12 constelaciones a lo largo de esa línea son conocidas como el zodíaco, un nombre que debe ser familiar a quienes siguen la astrología. Venus, el planeta más brillante, oscila hacia atrás y adelante a lo largo de la posición del Sol, y Mercurio también--pero debido a que está mucho más cercano al Sol, tan solo lo puede ver al estar lo más retirado del Sol, y por corto tiempo despues del ocaso o antes del amanecer.

    Los estudiantes probablemente habrán escuchado o leído que el Papa y la Iglesia pelearon contra la idea de Copérnico. Debido a que en uno de los Salmos (los cuales son en realidad oraciones-poemas), la Biblia dice que Dios, "puso la Tierra para que no se moviera" (esa fue una traducción: una más correcta es "no se colapsará"). Galileo, un Italiano contemporáneo de Kepler, quien apoyó las ideas de Copérnico, fue juzgado por la Iglesia por desobediencia y fue sentenciado a arresto domiciliario por el resto de su vida.

    Fue esta una época en la cual la gente con frecuencia seguía a los antiguos autores (como el Griego Aristóteles), en lugar de verificar con sus propios ojos, lo que la Naturaleza estaba haciendo en realidad. Cuando la gente comenzó a verificar, observar, experimentar y calcular, eso se convirtió en la revolución científica. Nuestra tecnología moderna es el resultado final, y las leyes de Kepler (junto con el trabajo de Galielo, y el de William Gilbert sobre el magnetismo) son importantes, debido a que ellas comenzaron la revolución.

Johannes  Kepler

    Kepler trabajó con Tycho Brahe, un noble Danés que llevó la astronomía pre-telescópica a su mayor precisión, midiendo las posiciones de los planetas de una manera tan exacta como el ojo lo permite (Brahe murió en 1602 en Praga, ahora la capital Checa; los telescopios comenzaron con Galileo alrededor de 1609). Si quiere leer al respecto, le recomiendo "Tycho and Kepler" por Kitty Ferguson, revisado en http://www.phy6.org/outreach/books/Tycho.htm, o por lo menos, lea la crítica. Permítame citar de él:

    La Intolerancia Religiosa estaba muy extendida--de hecho, los eventos se estaban encaminando hacia la guerra de los 30 años (1618-48), la batalla religiosa más destructora de Europa, reflejada por la guerra civil en Bretaña. Kepler fue forzado a salir de Graz, entre otros empleados de colegios Protestantes en la ciudad, después de que el gobernante archiduque decretó que deberían dejar la ciudad al caer la noche, ese mismo día. Era también una era en que la madre de Kepler fue arrestada por brujería, cuando la mayoría de sus numerosos hijos habían muerto en la niñez, y cuando el matrimonio de Tycho, el cual era visto como de segunda clase, con hijos de una mujer no casada, debido a que su esposa no era de la nobleza.

    Intente hacer ver eso a sus alumnos también. En 1620 fue cuando los "peregrinos" tocaron tierra en Plymouth Rock, huyendo del comienzo de la guerra religiosa que después devastó a Europa. Es muy probable que fue el recuerdo de dichas guerras que condujo a los Estados Unidos, tiempo después, a decretar la separación de la Iglesia y el Estado. Explique cómo el desarrollo de la ciencia y la sociedad casi siempre están muy relacionadas.

Primera Ley de Kepler

(1) Los planetas se mueven alrededor del Sol en elipses, con el Sol en un foco

Primero explique lo que es una elipse: una de las formas de las "secciones cónicas," obtenidas mediante el cortar un cono con una superficie plana. Una linterna crea un cono de luz: diríjala a una pared plana y obtiene una sección cónica.

Dirija el haz a la pared de forma perpendicular. La pared corta al cono de manera perpendicular al eje y así obtiene un círculo de luz.

Ponga el cono en ángulo relativo a la pared: una elipse. Entre mayor sea el ángulo, más lejos se cierra la elipse.

las curvas generadas como  "secciones cónicas" cuando planos rectos son cortados a lo largo de un cono.

Finalmente, si el eje del cono está paralelo a la pared, la curva nunca se cierra: se obtiene una parábola. Las leyes de Kepler (así las conocemos ahora) forman todas secciones cónicas, y las parábolas son muy parecidas a las órbitas de los cometas no periódicos, los cuales comienzan sus movimientos muy lejos.

(Incline aún más y obtendrá hipérbolas--no solo las trayectorias no se cierran, sino la direcciones de ir y venir forman un ángulo definido).

    Hay más, mucho más... pero tan solo déjeme traer a colación dos puntos. Son buenos puntos para participar en clase, porque unen el trabajo de Kepler de alrededor de 1610 con los últimos descubrimientos científicos del siglo 21.
    Primero que nada, una elipse muy famosa se muestra abajo. Su historia es narrada en al sección #S7-a

   Probablemente todos sepan que nuestro Sol es parte de una inmensa colección de estrellas en forma de disco--aproximadamente 100,000 millones de acuerdo al último conteo--llamada galaxia. Es un disco plano, una tortilla como el sistema solar--y en este caso también, vemos a esa tortilla de lado, de manera que también reduce nuestro campo de visión a una pequeña tira. En esa tira vemos una banda de estrellas débiles corriendo alrededor de la esfera celestial, la "Vía Láctea".

    ¿Qué mantiene unida a nuestra galaxia (y a las más distantes)? Se creyó por mucho tiempo que había un inmenso agujero negro en el centro, pero ese centro estaba oscurecido por nubes de polvo y por lo tanto no era fácil de observar. Recientemente fueron construídos telescopios de alta resolución, sensibles a la luz infraroja, los cuales pueden ver a través del polvo, y han mostrado una gran concentración de estrellas moviéndose rápidamente cerca del centro de la galaxia, en órbitas que obedecen las leyes de Kepler. Este sitio de la red muestra la elipse de una estrella orbitando al centro una vez cada 15.2 años, y los cálculos deducen una masa de aproximadamente 3.7 millones de soles, más menos 1.5 millones.

    [Solo para astrónomos: la masa central ayuda a mantener la galaxia unida, pero hay algo más que masa involucrada, porque la rotación de las partes más retiradas de las galaxias no obedecen la tercera ley de kepler. De hecho, sus partes principales parecen rotar como discos sólidos, lo cual es difícil de explicar a menos que asumamos que las galaxias contienen, además de estrellas brillantes, mucha "materia oscura", que afecta la gravedad pero es invisible. Vea la nota al final del artículo #20]

    En segundo lugar, dijimos que la Tierra orbita al Sol (y por cierto, las mismas leyes también aplican para los satélites artificiales que orbitan la Tierra). Pero imagine que pudiera hacer gradualmente que la Tierra fuera cada vez más pesada, y al mismo tiempo el Sol fuera cada vez más ligero. ¿Entonces qué? Al llegar al punto en donde la Tierra y el Sol pesaran lo mismo--¿quién orbita a quién?

    Aproximadamente 50 años después de Kepler, Isaac Newton explicó las leyes de Kepler (y al hacerlo, estableció con firmeza la "revolución científica" a partir de ese momento). Esto es lo que él hizo:

--- Primero obtuvo las leyes del movimiento--conocidas a partir de entonces como las "3 leyes de Newton del movimiento", y es problable que usted las imparta en clase, también.

---Segundo, nos dió la ley de la gravitación universal--mostrando que la misma fuerza que ocasiona que las manzanas y las piedras caigan, también mantiene a la Luna en su órbita-- y por lo tanto, probablemente, creó todas las órbitas del sistema solar.

   (Para ver más relativo a esto (inclusive de esa manzana), vea la sección #20 http://www.phy6.org/stargaze/Mgravity.htm)

--Y tercero, él probó que si los dos puntos anteriores eran válidos, la leyes de Kepler podían ser derivadas matemáticamente...

   ... pero con un pequeño cambio: los planetas no orbitan alrededor del Sol, sino alrededor de un centro común de gravedad. Mientras que la Tierra recorre un gran circuito cada año, el Sol también realiza uno, uno muy pequeño, alrededor del centro de gravedad del Sol-tierra.

(En realidad, el Sol también es movido por Júpiter, Saturno, etc, y el patrón resultante es complicado).

   ¿Porqué es esto importante? Porque nos ayuda a descubrir ¡si otras estrellas tienen planetas!. No podemos ver aquellos planetas--demasiado tenues--pero si la estrella presenta un vaivén de una forma complicada, puede ser que sea un planeta el que la mueva así.

   ¿Funciona esto? Sí y no (vea el fin del artículo #11a). Muchos planetas han sido descubiertos de esta forma, pero la mayoría de ellos están demasiado cerca a las estrellas (se mueven en una escala de tiempo de semanas) y son muy grandes. El descubrir planetas similares a la Tierra es difícil--el vaivén es más pequeño y necesitamos observarlo durante muchos años para obtener una periodicidad del orden de un año. Pero manténgase conectado, los astrónomos están trabajando en ello.
------------------

Segunda Ley de Kepler

(2) La línea que conecta el Sol con un planeta barre
        áreas iguales en tiempos iguales.

(Esa línea a veces es llamada "radio vector").

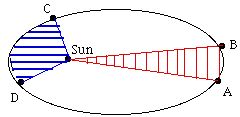Ilustrando la 2da. ley de Kepler:  A los segmentos AB y CD les lleva el  mismo tiempo el recorrerlo.

    Una elipse es un óvalo elongado simétrico, con dos focos localizados simétricamente hacia las orillas más "agudas"--un foco contiene al Sol, y el otro está vacío. (Dibuje dicha elipse). Si acercamos los focos cada vez más, la elipse se parece cada vez más a un círculo, y cuando se traslapan, finalmente tenemos un círculo.

    [La órbita de la Tierra, así como la mayoría de las órbitas planetarias, se aproximan mucho a un círculo. Si le mostrara la órbita de la Tierra sin el Sol en un foco, es probable que no pudiera distinguirla de un círculo. Con el Sol incluído, sin embargo, podrá notar que está ligeramente fuera de centro].

    La clave de la 2da. ley de Kepler es que, aunque la órbita es simétrica, el movimiento no lo es. Un planeta se acelera al acercarse al Sol, obtiene su máxima velocidad al pasar en su máxima aproximación, y luego se desacelera.

(La estrella S2 se acelera hasta un 2% de la velocidad de la luz al acercarse al agujero negro que está en el centro de nuestra galaxia).

   Lo que ocurre se entiende mejor en términos de energía. Conforme se retira el planeta del Sol (o el satélite de la Tierra), este pierde energía al sobreponerse de la atracción gravitacional, y se desacelera, como una piedra tirada hacia arriba. Y al igual que la piedra, vuelve a ganar su energía (completamente--no hay resistencia al aire en el espacio) al regresar.

   Hay un ejercicio fácil aquí, el cual está también en la sección #12A .

    Suponga que tiene un planeta cuyas distancias más pequeña/grande desde el centro son (r₁, r₂)--son llamados perihelio y efelio si el centro es el Sol, o (perigeo, apogeo) si el centro es la Tierra. (Las distancias siempre se miden desde el centro de los cuerpos, o desde los centros de gravedad).

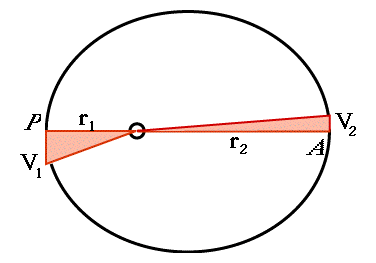
    Digamos que es un planeta que está orbitando el Sol. Entonces--la velocidad V₁ en perihelio es la más rápida de la órbita. Es por lo tanto, la distancia cubierta en un segundo en perihelio. La velocidad V₂ en afelio es la más lenta de la órbita. Es por lo tanto la distancia cubierta en un segundo en afelio.

El área barrida por el "radio vector" r durante un segundo después del perihelio es un triángulo rectángulo de base V₁, de manera que su área es 0.5 r₁ V₁

El área barrida por el "radio vecto" r durante un segundo después del afelio es un triángulo rectángulo de base V₂, de manera que su área es 0.5 r₂ V₂

De acuerdo a la ley de la áreas, ambas áreas son iguales, de manera que

    Si el afelio r₂ es 3 veces la distancia del perihelio, la velocidad V₂ en ese lugar es 3 veces más lenta. (Note: esta relación solo es válida en estos dos puntos de la órbita. En cualquier otro punto, la velocidad y el radio no son perpendiculares).
----------------

    ¿Estamos lo más cerca del Sol? Aproximadamente el 4 de Enero, en un 1.5%, no lo suficiente como para que el Sol se aprecie distinto.
    Esta es una forma rápida para demostrar esta asimetría (aunque probablemente no tenga tiempo para cubrirla en clase). Dibuje una elipse, con el eje largo y una línea perpendicular a dicho eje a través del Sol)
   .Entonces ocurre (pura casualidad) que el equinoccio de primavera y el de otoño, cuando el día y la noche son iguales, típicamente el 21 de Marzo, Septiembre 22 ó 23, caen muy cercanos a esta línea perpendicular.

   Observe la vista esquemática de la órbita de la Tierra en la sección #3. El eje largo (como se definió arriba) es la línea conectando Diciembre-Junio en ese dibujo, y la línea perpendicular es la que conecta Marzo-Septiembre.

    ¿Si la órbita fuera exactamente un círculo? (en cuyo caso, lo que llamamos "eje largo", sería completamente arbitrario, un diámetro igual que cualquier otro), entonces, de acuerdo a la segunda ley de Kepler, la Tierra se movería a una velocidad constante y pasaría el mismo tiempo en el verano que en el otoño. ¡De hecho, pasa aproximadamente dos días menos en la parte del invierno! (Tome un calendario y cuente los días de un equinoccio al otro). Eso puede significar que

   
• La parte del invierno es más corta, o
• La Tierra se mueve más rápido en la parte del invierno

En realidad, ambas condiciones son ciertas, si la Tierra está lo más cercana a Sol alrededor de Enero 4. La "mitad" de la elipse (determinada por la línea perpendicular definida arriba) que está más cercana al Sol es más pequeña (demuéstrelo con un dibujo de una elipse que sea notoriamente ovalada), y de acuerdo a la segunda ley de Kepler, la Tierra se mueve más rápida al estar más cerca del Sol.
-------------------------

    El hecho de que el hemisferio norte esté más cerca del Sol a mediados de invierno y lo más retirado a mediados del verano, hace que se moderen las estaciones, haciéndolas más suaves.
    En el hemisferio sur, los haría más crudos, aunque los grandes océanos ayudan a moderar su efecto.

    Pero el eje de la Tierra se mueva alrededor de un cono, con un ciclo de 26000 años. En 13000 años, estaremos lo más cerca del Sol a mediados del verano, y el clima se hará más extremo. De acuerdo a lo descrito en la sección 7, esto puede ser un efecto ligado a los orígenes de la edad de hielo, pero no tenemos tiempo para los detalles.

Tercera ley de Kepler

(3) El cuadrado del período orbital de un planeta es proporcional al cubo de la distancia media desde el Sol.

(O en otras palabras--del "eje semimayor" de la elipse, la mitad de la suma de la distancia más grande y la más pequeña desde el Sol).

   Esta es una ley matemática, y sus estudiantes necesitan calculadoras con raíces cuadradas, también potencias a la 3/2 y 2/3 (y tal vez también raíces cúbicas o potencias a la 1/3 que es lo mismo)...

    Si dos planetas (o dos satélites de la Tierra---funciona igual) tienen períodos orbitales T1 y T1 de días o años, y distancias medias desde el Sol (o ejes semimayores) A1 y A2, entonces la fórmula expresando la tercera ley es

    Los estudiantes preguntarán de inmediato--podemos contar días para obtener el período orbital T (aunque puede ser complicado, necesitamos restar el movimiento de la Tierra alrededor del Sol)--pero ¿Cómo conocemos las distancia A?

    En realidad, no la conocemos, pero observamos que solo se necesitan las proporciones de las distancias, y las unidades no afectan a las proporciones. Por ejemplo, suponga que "Planeta 2" es la Tierra, y todos los tiempos están en años. Entonces T₂=1 (año) y podemos medir todas las distancias en unidades astronómicas (UA), la distancia media Sol-Tierra, de manera que A₂ =1 (UA). La ley entonces aplica, para cualquier planeta,